Debaten la idea de Hawking de que el universo no tuvo un comienzo
- Alice Meraviglia

- Aug 31, 2021
- 13 min read
Updated: Jan 23, 2022
Por Natalie Walchover

Una reciente polémica sobre la mayor idea de Stephen Hawking de que el universo podría haber surgido de la nada ha puesto a los cosmólogos a elegir bandos.
En 1981, muchos de los principales cosmólogos del mundo se reunieron en la Academia Pontificia de las Ciencias, un vestigio de los linajes acoplados de la ciencia y la teología situado en una elegante villa en los jardines del Vaticano. Stephen Hawking eligió el augusto escenario para presentar lo que más tarde consideraría su idea más importante: una propuesta sobre cómo el universo podría haber surgido de la nada.
Antes de la charla de Hawking, todas las historias de origen cosmológico, científicas o teológicas, habían invitado a la réplica: "¿Qué pasó antes?". La teoría del Big Bang, por ejemplo -promovida 50 años antes de la conferencia de Hawking por el físico belga y sacerdote católico Georges Lemaître, que más tarde fue presidente de la academia de ciencias del Vaticano- retrotrae la expansión del universo a un haz de energía caliente y denso. Pero, ¿de dónde proviene esa energía inicial?
La teoría del Big Bang tenía otros problemas. Los físicos comprendieron que un bulto de energía en expansión crecería hasta convertirse en un desorden arrugado, en lugar del enorme y suave cosmos que observan los astrónomos modernos. En 1980, un año antes de la conferencia de Hawking, el cosmólogo Alan Guth se dio cuenta de que los problemas del Big Bang podían solucionarse con un añadido: un crecimiento inicial exponencial conocido como inflación cósmica, que habría hecho que el universo fuera enorme, liso y plano antes de que la gravedad tuviera la oportunidad de destrozarlo. La inflación se convirtió rápidamente en la principal teoría de nuestros orígenes cósmicos. Sin embargo, la cuestión de las condiciones iniciales seguía vigente: ¿Cuál fue el origen de la minúscula porción que supuestamente se convirtió en nuestro cosmos, y de la energía potencial que la infló?
Hawking, en su brillantez, vio una forma de acabar con el interminable tanteo hacia atrás en el tiempo: Propuso que no hay fin, o principio, en absoluto. Según el acta de la conferencia en el Vaticano, el físico de Cambridge, que entonces tenía 39 años y aún podía hablar con su propia voz, dijo a la multitud: "Debería haber algo muy especial en las condiciones en los límites del universo, y ¿qué puede ser más especial que la condición de que no haya límites?"
"Preguntar qué hubo antes del Big Bang... sería como preguntar qué hay al sur del Polo Sur." - Stephen Hawking

"Preguntar qué hubo antes del Big Bang no tiene sentido, según la propuesta sin límites, porque no hay ninguna noción de tiempo disponible a la que referirse", dijo Hawking en otra conferencia en la Academia Pontificia en 2016, un año y medio antes de su muerte. "Sería como preguntar qué hay al sur del Polo Sur".
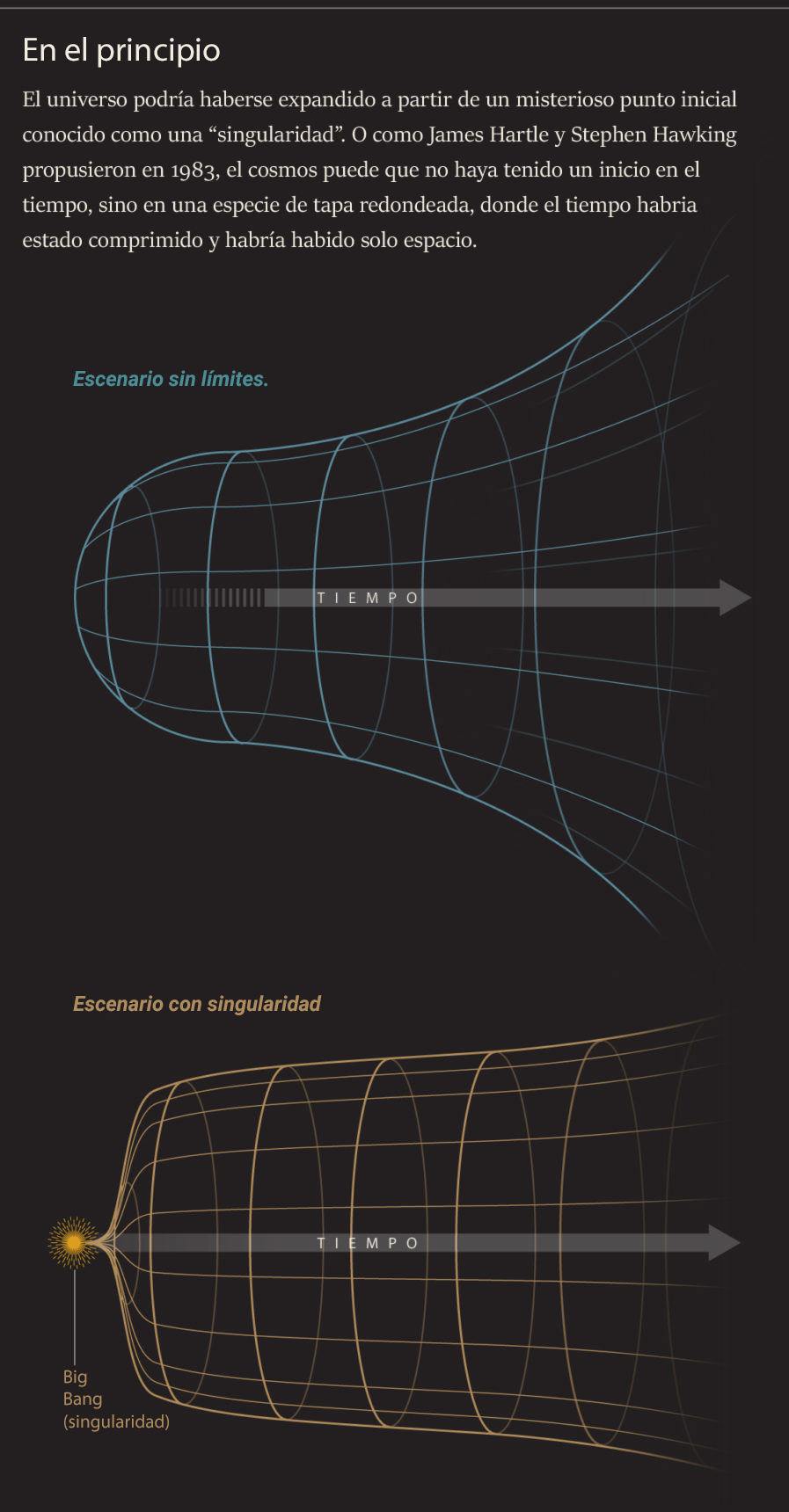
La propuesta de Hartle y Hawking reconceptualizó radicalmente el tiempo. Cada momento del universo se convierte en una sección transversal del volantito (la figura de la imagen al principio de este artículo); mientras que percibimos el universo como algo que se expande y evoluciona de un momento a otro, el tiempo consiste realmente en correlaciones entre el tamaño del universo en cada sección transversal y otras propiedades - particularmente su entropía, o desorden. La entropía aumenta desde el corcho hasta las plumas, apuntando una flecha emergente del tiempo. Sin embargo, cerca del fondo redondeado del volante, las correlaciones son menos fiables; el tiempo deja de existir y es sustituido por el espacio puro. Hartle, que ahora tiene 79 años y es profesor de la Universidad de California en Santa Bárbara, lo explicaba recientemente por teléfono: "No teníamos pájaros en el universo primitivo; los tenemos después. ... No teníamos tiempo en el universo primitivo, pero tenemos tiempo después".
La propuesta de no tener límites ha fascinado e inspirado a los físicos durante casi cuatro décadas. "Es una idea increíblemente bella y provocativa", afirma Neil Turok, cosmólogo del Instituto Perimetral de Física Teórica de Waterloo (Canadá) y antiguo colaborador de Hawking. La propuesta representaba una primera conjetura sobre la descripción cuántica del cosmos: la función de onda del universo. Pronto surgió todo un campo, la cosmología cuántica, a medida que los investigadores ideaban ideas alternativas sobre cómo el universo podría haber surgido de la nada, analizaban las diversas predicciones de las teorías y las formas de probarlas, e interpretaban su significado filosófico. La función de onda sin límites, según Hartle, "era en cierto modo la propuesta más sencilla posible para ello".
Pero hace dos años, un artículo de Turok, Job Feldbrugge, del Instituto Perimeter, y Jean-Luc Lehners, del Instituto Max Planck de Física Gravitacional de Alemania, puso en duda la propuesta de Hartle-Hawking. La propuesta, por supuesto, sólo es viable si un universo que se curva a partir de un punto sin dimensiones de la forma en que Hartle y Hawking imaginaron crece naturalmente hasta convertirse en un universo como el nuestro. Hawking y Hartle argumentaron que sí, que los universos sin límites tenderán a ser enormes, asombrosamente suaves, impresionantemente planos y en expansión, al igual que el cosmos real. "El problema del planteamiento de Stephen y Jim es que era ambiguo", dijo Turok, "profundamente ambiguo".
"Murray Gell-Mann solía preguntarme: "Si conoces la función de onda del universo, ¿por qué no eres rico?" - James Hartle
En su artículo de 2017, publicado en Physical Review Letters, Turok y sus coautores abordaron la propuesta sin límites de Hartle y Hawking con nuevas técnicas matemáticas que, en su opinión, hacen que sus predicciones sean mucho más concretas que antes. "... pero descubrimos que fallaba estrepitosamente", dijo Turok. "Sencillamente, no era posible, desde el punto de vista de la mecánica cuántica, que un universo comenzara de la forma que ellos imaginaban". El trío comprobó sus matemáticas y cuestionó sus supuestos subyacentes antes de hacerlo público, pero "por desgracia", dijo Turok, "parecía ineludible que la propuesta de Hartle-Hawking era un desastre."
El artículo suscitó una controversia. Otros expertos defendieron enérgicamente la idea de la ausencia de límites y rebatieron el razonamiento de Turok y sus colegas. "No estamos de acuerdo con sus argumentos técnicos", dijo Thomas Hertog, físico de la Universidad Católica de Lovaina (Bélgica) que colaboró estrechamente con Hawking durante los últimos 20 años de su vida. "Pero, fundamentalmente, no estamos de acuerdo también con su definición, su marco, su elección de principios. Y esa es la discusión más interesante".
Después de dos años de enfrentamiento, los grupos han trasladado su desacuerdo técnico a las diferentes creencias sobre el funcionamiento de la naturaleza. El acalorado -aunque amistoso- debate ha contribuido a consolidar la idea que más le gustaba a Hawking. Incluso los detractores de su fórmula específica y la de Hartle, como Turok y Lehners, están elaborando modelos de cosmología cuántica competitivos que intentan evitar los supuestos escollos del original sin perder su ilimitado encanto.
El jardín de las delicias cósmicas
Hartle y Hawking se veían mucho a partir de los años 70, normalmente cuando se reunían en Cambridge para colaborar durante largos periodos. Las investigaciones teóricas del dúo sobre los agujeros negros y las misteriosas singularidades en sus centros les habían llevado a preguntarse por nuestro origen cósmico.
En 1915, Albert Einstein descubrió que las concentraciones de materia o energía deforman el tejido del espacio-tiempo, provocando la gravedad. En la década de 1960, Hawking y el físico de la Universidad de Oxford Roger Penrose demostraron que cuando el espacio-tiempo se curva lo suficientemente pronunciado, como en el interior de un agujero negro o quizás durante el Big Bang, inevitablemente se colapsa, curvándose infinitamente hacia una singularidad, donde las ecuaciones de Einstein se rompen y se necesita una nueva teoría cuántica de la gravedad. Los "teoremas de la singularidad" de Penrose-Hawking significaban que no había forma de que el espacio-tiempo comenzara suavemente, sin dramatismo, en un punto.
Así, Hawking y Hartle se vieron llevados a reflexionar sobre la posibilidad de que el universo comenzara como un espacio puro, en lugar de un espacio-tiempo dinámico. Y esto les llevó a la geometría del volantín. Definieron la función de onda sin límites que describe ese universo utilizando un enfoque inventado por el héroe de Hawking, el físico Richard Feynman. En la década de 1940, Feynman ideó un esquema para calcular los resultados más probables de los sucesos de la mecánica cuántica. Para predecir, por ejemplo, los resultados más probables de la colisión de una partícula, Feynman descubrió que se podían sumar todas las trayectorias posibles que podían tomar las partículas en colisión, ponderando más las trayectorias sencillas que las enrevesadas en la suma. Calculando esta "integral de trayectorias" se obtiene la función de onda: una distribución de probabilidad que indica los diferentes estados posibles de las partículas tras la colisión.
Del mismo modo, Hartle y Hawking expresaron la función de onda del universo -que describe sus estados probables- como la suma de todas las formas posibles en que podría haberse expandido fluidamente desde un punto. La esperanza era que la suma de todas las posibles "historias de expansión", universos de fondo liso de todas las formas y tamaños diferentes, diera como resultado una función de onda que diera una alta probabilidad a un universo enorme, liso y plano como el nuestro. Si la suma ponderada de todas las historias de expansión posibles arroja algún otro tipo de universo como resultado más probable, la propuesta sin límites fracasa.
El problema es que la integral de trayectorias sobre todas las posibles historias de expansión es demasiado complicada de calcular con exactitud. Son posibles innumerables formas y tamaños diferentes de universos, y cada uno de ellos puede ser un asunto enmarañado. "Murray Gell-Mann solía preguntarme", dijo Hartle, refiriéndose al difunto físico ganador del Premio Nobel, "si conoces la función de onda del universo, ¿por qué no eres rico?". Por supuesto, para resolver realmente la función de onda utilizando el método de Feynman, Hartle y Hawking tuvieron que simplificar drásticamente la situación, ignorando incluso las partículas específicas que pueblan nuestro mundo (lo que significaba que su fórmula no estaba ni cerca de poder predecir el mercado de valores). Consideraron la integral de la trayectoria sobre todos los posibles universos de juguete en el "minisuperespacio", definido como el conjunto de todos los universos con un único campo de energía que los atraviesa: la energía que impulsó la inflación cósmica. (En la imagen del volante de Hartle y Hawking, ese período inicial de inflado corresponde al rápido aumento del diámetro cerca del fondo del corcho).
Incluso el cálculo del minisuperespacio es difícil de resolver con exactitud, pero los físicos saben que hay dos posibles historias de expansión que dominan potencialmente el cálculo. Estas formas de universo rivales anclan los dos lados del debate actual.
" [Stephen Hawking] probablemente tenía la mejor intuición de todos en estos temas. Pero no siempre tenía razón." - Neil Turok
Las soluciones rivales son las dos historias de expansión "clásicas" que puede tener un universo. Después de una inflación cósmica inicial desde el tamaño cero, estos universos se expanden constantemente según la teoría de la gravedad y el espacio-tiempo de Einstein. Las historias de expansión más extrañas, como los universos con forma de fútbol o de oruga, se anulan en su mayoría en el cálculo cuántico.
Una de las dos soluciones clásicas se parece a nuestro universo. A gran escala, es suave y está salpicado de energía al azar, debido a las fluctuaciones cuánticas durante la inflación. Como en el universo real, las diferencias de densidad entre las regiones forman una curva de campana en torno a cero. Si esta posible solución domina efectivamente la función de onda del minisuperespacio, resulta plausible imaginar que una versión mucho más detallada y exacta de la función de onda sin límites podría servir como modelo cosmológico viable del universo real.
La otra forma de universo potencialmente dominante no se parece en nada a la realidad. A medida que se ensancha, la energía que lo infunde varía de forma cada vez más extrema, creando enormes diferencias de densidad de un lugar a otro que la gravedad empeora constantemente. Las variaciones de densidad forman una curva de campana invertida, en la que las diferencias entre regiones no se acercan a cero, sino al infinito. Si éste es el término dominante en la función de onda sin límites para el minisuperespacio, entonces la propuesta de Hartle-Hawking parece estar equivocada.
Las dos historias de expansión dominantes presentan una elección en cuanto a cómo debe hacerse la integral de trayectoria. Si las historias dominantes son dos localizaciones en un mapa, megaciudades en el reino de todos los universos mecánicos cuánticos posibles, la cuestión es qué camino debemos tomar a través del terreno. ¿Qué historia de expansión dominante, y sólo puede haber una, debe recoger nuestro "contorno de integración"? Los investigadores se han bifurcado por diferentes caminos.
En su artículo de 2017, Turok, Feldbrugge y Lehners tomaron un camino a través del jardín de posibles historias de expansión que llevó a la segunda solución dominante. En su opinión, el único contorno sensato es el que recorre los valores reales (en contraposición a los valores imaginarios, que implican las raíces cuadradas de los números negativos) para una variable llamada "lapso". El lapso es esencialmente la altura de cada universo posible de volantes: la distancia que se necesita para alcanzar un determinado diámetro. Al carecer de un elemento causal, el lapso no es nuestra noción habitual de tiempo. Sin embargo, Turok y sus colegas argumentan, en parte por motivos de causalidad, que sólo los valores reales del lapso tienen sentido físico. Y la suma de los universos con valores reales de lapso conduce a una solución físicamente absurda y muy fluctuante.
" La gente confía mucho en la intuición de Stephen ", dijo Turok por teléfono. "Por una buena razón - quiero decir, él probablemente tenía la mejor intuición de todos en estos temas. Pero no siempre tenía razón". - Neil Turok
Universos imaginarios
Jonathan Halliwell, físico del Imperial College de Londres, ha estudiado la propuesta de los no límites desde que era alumno de Hawking en la década de 1980. Él y Hartle analizaron la cuestión del contorno de la integración en 1990. En su opinión, al igual que en la de Hertog y, aparentemente, en la de Hawking, el contorno no es fundamental, sino una herramienta matemática que se puede aprovechar al máximo. Es similar a cómo la trayectoria de un planeta alrededor del sol puede expresarse matemáticamente como una serie de ángulos, como una serie de tiempos, o en términos de cualquiera de otros parámetros convenientes. "Se puede hacer esa parametrización de muchas maneras diferentes, pero ninguna de ellas es más física que otra", dijo Halliwell.
Él y sus colegas sostienen que, en el caso del minisuperespacio, sólo tienen sentido los contornos que recogen la historia buena de la expansión. La mecánica cuántica exige que las probabilidades sumen 1, o que sean "normalizables", pero el universo salvajemente fluctuante en el que aterrizó el equipo de Turok no lo es. Esa solución no tiene sentido, está plagada de infinitos y no está permitida por las leyes cuánticas -señales obvias, según los defensores del no-límite, de que hay que ir por otro camino.

Es cierto que los contornos que pasan por la solución buena suman posibles universos con valores imaginarios para sus variables de lapso. Pero aparte de Turok y compañía, poca gente cree que eso sea un problema. Los números imaginarios impregnan la mecánica cuántica. Para el equipo de Hartle-Hawking, los críticos invocan una falsa noción de causalidad al exigir que el lapso sea real. "Ese es un principio que no está escrito en las estrellas, y con el que estamos profundamente en desacuerdo", dijo Hertog.
Según Hertog, Hawking rara vez mencionó la formulación de la integral de trayectoria de la función de onda sin límites en sus últimos años, en parte debido a la ambigüedad en torno a la elección del contorno. Consideraba que la historia de la expansión normalizable, que la integral de trayectoria sólo había ayudado a descubrir, era la solución a una ecuación más fundamental sobre el universo planteada en la década de 1960 por los físicos John Wheeler y Bryce DeWitt. Wheeler y DeWitt -tras reflexionar sobre la cuestión durante una escala en el aeropuerto internacional de Raleigh-Durham- argumentaron que la función de onda del universo, sea cual sea, no puede depender del tiempo, ya que no existe un reloj externo con el que medirla. Y, por tanto, la cantidad de energía en el universo, cuando se suman las contribuciones positivas y negativas de la materia y la gravedad, debe permanecer en cero para siempre. La función de onda sin límites satisface la ecuación de Wheeler-DeWitt para el minisuperespacio.
En los últimos años de su vida, para comprender mejor la función de onda de forma más general, Hawking y sus colaboradores comenzaron a aplicar la holografía, un nuevo y exitoso enfoque que trata el espacio-tiempo como un holograma. Hawking buscaba una descripción holográfica de un universo con forma de transbordador, en el que la geometría de todo el pasado se proyectara desde el presente.
Ese esfuerzo continúa en ausencia de Hawking. Pero Turok considera que este cambio de énfasis cambia las reglas. Al alejarse de la formulación de la integral de la trayectoria, dice, los defensores de la idea de no tener límites la han dejado mal definida. En su opinión, lo que están estudiando ya no es Hartle-Hawking, aunque el propio Hartle no esté de acuerdo.
Durante el último año, Turok y sus colegas del Instituto Perimeter, Latham Boyle y Kieran Finn, han estado desarrollando un nuevo modelo cosmológico que tiene mucho en común con la propuesta sin límites. Pero en lugar de un volante, prevé dos, dispuestos corcho con corcho en una especie de figura de reloj de arena con el tiempo fluyendo en ambas direcciones. Aunque el modelo aún no está lo suficientemente desarrollado como para hacer predicciones, su encanto reside en la forma en que sus lóbulos realizan la simetría CPT, un espejo aparentemente fundamental en la naturaleza que refleja simultáneamente la materia y la antimateria, a izquierda y derecha, y hacia delante y hacia atrás en el tiempo. Una desventaja es que los lóbulos especulares del universo se encuentran en una singularidad, un pellizco en el espacio-tiempo que requiere la desconocida teoría cuántica de la gravedad para entenderlo. Boyle, Finn y Turok hacen una apuesta por la singularidad, pero este intento es intrínsecamente especulativo.
También ha resurgido el interés por la "propuesta del túnel", una forma alternativa de que el universo pueda haber surgido de la nada, concebida en los años 80 de forma independiente por los cosmólogos ruso-americanos Alexander Vilenkin y Andrei Linde. La propuesta, que difiere de la función de onda sin límites principalmente por el signo menos, presenta el nacimiento del universo como un evento mecánico cuántico de "tunelización", similar a cuando una partícula aparece más allá de una barrera en un experimento mecánico cuántico.
Abundan las preguntas sobre cómo se cruzan las distintas propuestas con el razonamiento antrópico y la infame idea del multiverso. La función de onda sin límites, por ejemplo, favorece los universos vacíos, mientras que se necesitan materia y energía significativas para potenciar la enormidad y la complejidad. Hawking argumentó que la gran variedad de universos posibles que permite la función de onda debe realizarse en un multiverso mayor, dentro del cual sólo los universos complejos como el nuestro tendrán habitantes capaces de realizar observaciones. (El debate reciente se refiere a si estos universos complejos y habitables serán suaves o tendrán fluctuaciones salvajes). Una de las ventajas de la propuesta del túnel es que favorece a los universos llenos de materia y energía como el nuestro sin recurrir al razonamiento antrópico -aunque los universos que entran en túnel pueden tener otros problemas.
Sea como fuere, quizá nos quedemos con alguna esencia del cuadro que Hawking pintó por primera vez en la Academia Pontificia de Ciencias hace 38 años. O tal vez, en lugar de un no-principio como el del Polo Sur, el universo surgió de una singularidad después de todo, exigiendo un tipo diferente de función de onda. En cualquier caso, la búsqueda continuará. "Si estamos hablando de una teoría mecánica cuántica, ¿qué otra cosa hay que encontrar aparte de la función de onda?", se pregunta Juan Maldacena, un eminente físico teórico del Instituto de Estudios Avanzados de Princeton (Nueva Jersey), que se ha mantenido al margen de la reciente contienda. La cuestión de la función de onda del universo "es el tipo de pregunta correcta", dijo Maldacena, quien, por cierto, es miembro de la Academia Pontificia. "Si estamos encontrando la función de onda correcta, o cómo debemos pensar en la función de onda, es menos claro".



























Comments